《4.3 线段的长短比较》基础训练
1. 为比较两条线段AB与CD的大小,小明将点A与点C重合使两条线段在一条直线上,点B在CD的延长线上,则.
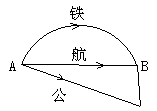
A. AB>CD B. AB 2. 如图①,把弯曲的河道改直,可以缩短航程,如此做的依据是. 图① A.两点之间,直线最短 B.两点确定一条线段 C.两点确定一条直线 D.两点之间,线段最短 3. 若线段AB=5 cm,CD=50 mm,则下列判断正确的是. A.AB=CD B.AB>CD C.AB<CD D.不可以确定 4. 如图②,已知线段AD>BC,则线段AC与BD的关系是. A.AC>BD B.AC=BD C.AC<BD D.不可以确定 图② 5. 两点间的距离是指. A.一条直线的长度 B.一条射线的长度 C.连接两点的线段 D.连接两点线段的长度 6. 如图③,下列关系式中与图形不符的式子是. 图③ A.AD-CD=AB+BC B.AC-BC=AD-BD C.AC-AB=AD-BD D.AD-AC=BD-BC 7. 下列说法中正确的是. A.延长射线OA B.作直线AB的延长线 C.延长线段AB到C,使AC= 8. 如图④,由A到B有①②③④四条路线,那样最短的路线是. 图④ A. ① B. ② C. ③ D. ④ 9. 如图⑤,C是AB的中点,D是BC的中点.下面等式不正确的是. 图⑤ A. CD=AC-DB B. CD=AD-BC C. CD= 10. 把一段弯曲的公路改为直路,可以缩短路程,其理由是. A. 两点之间线段最短 B. 两点确定一条直线 C. 线段有两个端点 D. 线段可以比较大小 11. 如图⑥,线段AC=BD,那样AB=________. 图⑥ 12. 线段的中点只有________个,线段的五等分点有________个. 13. 如图⑦,从城市A到城市B有三种不一样的交通工作:汽车、火车、飞机,除去速度原因,坐飞机的时间最短是由于___________. 图⑦ 14. 如图⑧,请依据图形完成下列填空: 图⑧ AD=AC+_________; AC=AB-_______=AD-_______; AC+CB=AD+________. 15. 两根木条,一根长80 cm,一根长120 cm,将它们的一端重合,顺次放在同一条直线上,此时两根木条的中点间的距离是多少? 答案和分析 【答案】 1. A 2. D 3. A 4. A 5. D 6. B 7. D 8. B 9. D 10. A 11. CD 12. 1 5 13. 两点之间,线段最短 14. CD BC CD BD 15. 100cm. 【分析】 1. 解:由点A与点C重合使两条线段在一条直线上,点B在CD的延长线上,得AB>CD.故选A. 比较线段长短时,叠合法是一种较为常见的办法. 2. 解:把弯曲的河道改直缩短航程的依据是:两点之间,线段最短. 故选D. 本题考查了线段的性质,熟记两点之间线段最短是解题的重点. 3. 解:CD=50 mm=5 cm,AB=5 cm,故AB=CD. 故选A. 本题考查了比较线段的长短的常识,解题重点是将线段的单位统一后再进行比较. 4. 解:由于AD>BC, 所以AC+CD>BD+CD, 所以AC>BD, 故选A. 本题考查了比较线段的长短的常识,解题重点是由已知得到AC+CD>BD+CD. 5. 解:两点间的距离是指连接两点线段的长度. 故选D. 此题考查的是两点间的距离的概念,连结两点的线段的长度叫做两点之间的距离. 6. 解:AD-CD=AC=AB+BC,故A正确; AC-BC=AB=AD-BD,故B正确; AC-AB=BC,AD-BD=AB,故C错误; AD-AC=CD=BD-BC,故D正确. 故选C. 本题考查了线段的和差,解题重点是找出线段之间的等量关系. 7. 解:射线、直线是不可度量的,没办法“延长”,故A、B错误; 延长线段AB到C,则AC>AB,故C错误,D正确. 故选D. 本题考查了对线段、射线、直线的语言描述,是基础题. 8. 解:依据两点之间,线段最短,则最短路线为路线②, 故选B. 本题考查了线段的性质,熟记两点之间线段最短是解题的重点. 9. 解:由于C是AB的中点,所以AC=BC= 又由于D是BC的中点,所以CD=BD= 所以CD=BC-DB=AC-DB,故A正确; CD=AD-AC=AD-BC,故B正确; CD=BC-DB= CD= 故选D. 本题考查了线段的和差,注意理解线段的中点的定义,借助中点的性质转化线段之间的倍分关系是解题的重点. 10. 解:由把弯曲的公路改为直路,路程变短了可知,应用了“两点之间线段最短”. 故选A. 本题考查了线段的性质,熟记两点之间线段最短是解题的重点. 11. 解:由图可知,AB=AC-BC,CD=BD-BC, 由于AC=BD,所以AB=CD. 故答案为CD. 本题考查了线段的和差,解题重点是找到线段之间的等量关系. 12. 解:线段的中点只有1个,线段的五等分点有4个. 故答案为1,5. 此题考查的是对线段的中点和等分点的认识,若将线段n等分,则线段的等分点有个. 13. 解:从城市A到城市B有三种不一样的交通工作:汽车、火车、飞机,除去速度原因,坐飞机的时间最短是由于两点之间,线段最短. 故答案为两点之间,线段最短. 本题考查了线段的性质,熟记两点之间线段最短是解题的重点. 14. 解:AD=AC+CD; AC=AB-BC=AD-CD; AC+CB=AD+BD. 故答案为CD; BC,CD;BD. 本题考查了线段的和差,解题重点是找到线段之间的等量关系. 15. 解:由题意,得80 cm的一半是40 cm,120 cm的一半是60 cm,故两根木条的中点间的距离是40+60=100. 本题考查了线段的中点的定义,借助中点的性质转化线段之间的倍分关系是解题的重点. 《4.3 线段的长短比较》提升训练 1. 如图①,若点C为线段AB上一点,且AB=16,AC=10,则AB的中点D与BC的中点E的距离为. 图① A.8 B.5 C.3 D.2 2. 下列说法正确的是. A. 两点之间的所有连线中,直线最短 B. 若P是线段AB的中点,则AP=BP C. 若AP=BP,则P是线段AB的中点 D. 两点之间的线段叫作这两点之间的距离 3. 如图②,AB=12 cm,点C是AB的中点,点D是BC的中点,则AD的长为. 图② A.3 cm B.6 cm C.9 cm D.7.5 cm 4. 假如点B在线段AC上,那样下列各表达式中:①AB= A.1个 B.2个 C.3个 D.4个 5. 如图③,笔直公路的同旁边有三棵树A,B,C,量得A,B两棵树之间的距离为5米,B,C两棵树之间的距离为3米,一个公路路标恰好在A,C两棵树的正中间点O处,则点O与点B之间的距离是. 图③ A.1米 B.2米 C.3米 D.4米 6. 点A,B,C在同一条直线上,线段AB=5 cm,线段BC=2 cm,则A,C两点间的距离是. A.3.5cm B.3cm C.7cm D.7cm或3cm 7. 已知:线段AB=4cm,延长AB至点C,使AC=11cm.点D是AB中点,点E是AC中点,则DE的长为. A.3.5cm B.3cm C.4cm D.4.5cm 8. 如图④,一只蚂蚁从A处沿着圆柱的表面爬到B处,请画出示意图且标出最短路线,并说明理由. 图④ 9. 如图⑤,李明想从A村到B村,你能帮他找到一条近期的路线吗?请说明理由. 图⑤ 10. 如图⑥,AB=16cm,C是AB上的一点,且AC=10cm,D是AC的中点,E是BC的中点,求线段DE的长. 答案和分析 【答案】 1. B 2. B 3. C 4. C 5. A 6. D 7. A 8. 线段AB即为最短路线. 9. 能,近期的路线为A→C→F→B. 10. 8cm. 【分析】 1. 解:由于AB=16,AC=10, 所以CB=AB-AC=16-10=6. 又由于D是AB中点,E是BC中点, 所以BD= 所以DE=BD-BE=8-3=5. 故选B. 本题考查了线段的和差,注意理解线段的中点的定义,借助中点的性质转化线段之间的倍分关系是解题的重点. 2. 解:两点之间的所有连线中,线段最短,故A选项错误; 当P是线段AB的中点时,AP=BP,但只了解AP=BP,不可以判断P是线段AB的中点,故B选项正确,C选项错误; 两点之间线段的长度叫作这两点之间的距离,故D选项错误. 故选B. 本题主要考查了线段的基本性质,线段的中点的概念与两点之间的距离的概念,数目学会这类定义和性质是解题重点. 3. 解:由于AB=12 cm,点C是AB的中点, 所以AC=BC= 又由于点D是BC的中点, 所以CD=BD= 所以AD=AB-BD=12-3=9, 故选C. 本题考查了线段的和差,注意理解线段的中点的定义,借助中点的性质转化线段之间的倍分关系是解题的重点. 4. 解:假如点B在线段AC上,能表示点B是线段AC的中点的有:①AB= 故选C. 此题考查的是线段的中点的概念,解题重点是熟练学会线段的中点的断定. 5. 解:依据题意可知,AB=5m,BC=3m,点O是线段AC的中点, 则OC= 所以OB=OC-BC=4-3=1, 故点O与点B之间的距离是1m. 故选A. 本题考查了线段的和差,注意理解线段的中点的定义,借助中点的性质转化线段之间的倍分关系是解题的重点. 6. 解:已知AB=5 cm,BC=2 cm, 当点B在点A、C之间时,AC=AB+BC=5+2=7; 当点C在点A、B之间时,AC=AB-BC=5-2=3, 故A,C两点间的距离是7cm或3cm. 故选D. 此题考查的是线段的和差,需要分两种状况进行讨论:点B在点A、C之间;点C在点A、B之间. 7. 解:由于AB=4cm,点D是AB中点,所以AD=2cm. 由于AC=11cm,点E是AC中点,所以AE=5.5cm. 所以DE=AE-AD=5.5-2=3.5cm 故选A. 本题考查了线段的和差,注意理解线段的中点的定义,借助中点的性质转化线段之间的倍分关系是解题的重点. 8. 解:将圆柱沿过点A的高剪开,侧面展开成平面图形,如图4. 由于两点之间线段最短,所以线段AB即为最短路线. 将圆柱沿着过点A的高剪开,侧面展开成平面图形,再依据线段的性质即可得到最短路线. 本题考查了线段的性质,熟记两点之间线段最短是解题的重点. 9. 解:能,近期的路线为A→C→F→B. 理由如下: 由于从A村到C村的距离是肯定的, 所以从A村到B村的远近取决于C村到B村的距离.把C,B看成两个点.由于两点之间线段最短,且F在线段CB上,所以从C到F再到B最 近.所以近期的路线为A→C→F→B. 本题考查了线段的性质,熟记两点之间线段最短是解题的重点.剖析出“从A村到B村的远近取决于C村到B村的距离”. 10. 解:解法1、由于D是AC中点,AC=10 cm,所以DC= 又由于AB=16 cm,AC=10 cm,所以BC=AB-AC=16-10=6. 又由于E是BC的中点, 所以CE= 所以DE=DC+CE=5+3=8. 解法2、由于D是AC的中点,E是BC的中点,所以DC= 所以DE=DC+CE= 由上可得DE的长为8 cm. 可以运用中点的概念先求出线段DC和CE的长,再求其和;也可以运用中点的概念直接得DE=DC+CE= 对于求线段的长度问题,解法不唯一,应依据具体的题目,灵活选择简单的计算办法. 《4.3 线段的长短比较》培优训练 1. 点M,N都在线段AB上,且M分AB为2 : 3两部分,N分AB为3 : 4两部分,若MN=2 cm,则AB的长为 A.60 cm B.70 cm C.75 cm D.80 cm 2. C、D是线段AB上顺次两点,M、N分别是AC、BD中点,若CD=a,MN=b,则AB的长为. A.2b-a B.b-a C.b+a D.2a+2b 3. 延长线段AB到点C,使BC= A.3 cm B.2 cm C.2.5 cm D.3.5 cm 4. 已知线段AB=2cm,延长AB到C,使BC=2AB,若D为AB的中点,则线段DC的长为______. 5. 如图,B,C两点把线段AD分成2 : 3 : 4的三部分,点E是线段AD的中点,EC=2 cm,求:AD的长;AB : BE. 答案和分析 【答案】 1. B 2. A 3. B 4. 5cm 5. 36cm;4 : 5. 【分析】 1. 解:由于M分AB为2 : 3两部分,N分AB为3 : 4两部分, 所以AM= 所以MN=AN-AM= 又由于MN=2 cm, 所以AB=70cm. 故选B. 依据线段的比可得,AM= 此题考查的是线段的比和线段的和差,熟练学会比的意义是解题的重点. 2. 解:由于C、D是线段AB上顺次两点,M、N分别是AC、BD中点, 所以AM=CM= 所以MN=CM+CD+DN, 由于CD=a,MN=b, 所以CM+DN=b-a,即 所以AC+BD=2, 所以AB=AC+CD+BD=2+a=2b-a. 故选A. 本题考查了线段的和差,注意理解线段的中点的定义,借助中点的性质转化线段之间的倍分关系是解题的重点. 3. 解:由于BC= 所以DC=DA+AB+BC= 由于DC=6 cm,所以AB=3cm, 所以DA=1cm, 又由于点E是线段DC的中点, 所以DE= 所以AE=DE-DA=3-1=2, 故线段DC的中点E和点A之间的距离为2 cm, 故选B. 本题考查了线段的和差,注意理解线段的中点的定义,借助中点的性质转化线段之间的倍分关系是解题的重点. 4. 解:由于AB=2cm,BC=2AB,所以BC=4cm, 又由于D为AB的中点, 所以AD=BD= 所以DC=BD+BC=1+4=5. 故答案为5cm. 本题考查了线段的和差,注意理解线段的中点的定义,借助中点的性质转化线段之间的倍分关系是解题的重点. 5. 解:设AB=2x,则BC=3x,CD=4x. 由线段的和差,得AD=AB+BC+CD=9x. 由E为AD的中点,得ED= 由线段的和差,得CE=DE-CD= 解得x=4. 所以AD=9x=36. AB=2x=8,BC=3x=12. 由线段的和差,得BE=BC-CE=12-2=10. 所以AB : BE=8 : 10=4 : 5. 依据线段的比,可设出未知数x,依据线段的和差,可得方程,依据解方程,可得x的值,依据x的值,可得AD的长度;依据线段的和差,可得线段BE的长,依据比的意义,可得答案. 在遇见线段之间比的问题时,总是设出未知数,列方程解答. 
![]()
![]()
![]() AB. D.延长线段AB到C,使AC=2AB.
AB. D.延长线段AB到C,使AC=2AB. 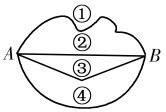
![]()
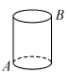
![]() AB-BD D. CD=
AB-BD D. CD=![]() AB
AB 
![]()
![]() AB,
AB, ![]() BC,
BC, ![]() AB-BD,故C正确;
AB-BD,故C正确; ![]() BC=
BC=![]() AB,故D错误.
AB,故D错误. ![]()
![]()
![]() AC;②AB=BC;③AC=2AB;④AB+BC=AC.能表示点B是线段AC的中点的有.
AC;②AB=BC;③AC=2AB;④AB+BC=AC.能表示点B是线段AC的中点的有. 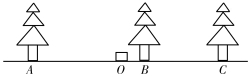
![]()
图⑥ 
![]() AB=
AB=![]() ×16=8,BE=
×16=8,BE=![]() CB=
CB=![]() ×6=3,
×6=3, ![]() AB=6cm,
AB=6cm, ![]() BC=3cm,
BC=3cm, ![]() AC;②AB=BC;③AC=2AB. 共3个.
AC;②AB=BC;③AC=2AB. 共3个. ![]() AC=
AC=![]() =
=![]() ×=4,
×=4, 
![]() AC=5 cm.
AC=5 cm. ![]() BC=3.
BC=3. ![]() AC,CE=
AC,CE=![]() BC,
BC, ![]() AC+
AC+![]() BC=
BC=![]() =
=![]() AB=
AB=![]() ×16=8.
×16=8. ![]() AC+
AC+![]() BC=
BC=![]() =
=![]() AB,再代入数即可.
AB,再代入数即可. ![]() AB,延长BA到点D,使DA=
AB,延长BA到点D,使DA=![]() AB,已知DC=6 cm,线段DC的中点E和点A之间的距离为.
AB,已知DC=6 cm,线段DC的中点E和点A之间的距离为. ![]()
![]() AB,AN=
AB,AN=![]() AB,
AB, ![]() AB-
AB-![]() AB=
AB=![]() AB,
AB, ![]() AB,AN=
AB,AN=![]() AB,则可以求出MN与AB之间的关系,借助已知条件MN=2 cm,即可得到AB的长度.
AB,则可以求出MN与AB之间的关系,借助已知条件MN=2 cm,即可得到AB的长度. ![]() AC,BN=DN=
AC,BN=DN=![]() BD,
BD, ![]() AC+
AC+![]() BD=b-a,
BD=b-a, ![]() AB,DA=
AB,DA=![]() AB,
AB, ![]() AB+AB+
AB+AB+![]() AB=2AB,
AB=2AB, ![]() DC=3cm,
DC=3cm, ![]() AB=1cm,
AB=1cm, ![]() AD=
AD=![]() x.
x. ![]() x-4x=
x-4x=![]() x=2.
x=2.







